|
|
# Estimation of the Laser Plane position
|
|
# Estimation of the Laser Plane position
|
|
|
---
|
|
---
|
|
|
We will use pinhole camera model for finding 3D points 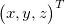 in projection coordinate 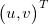 described as:
|
|
We will use pinhole camera model for finding 3D points in camera coordinate system 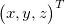 in projection coordinate 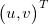 described as:
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/hbtk24o.png" /> ,
|
|
<img src="http://mathurl.com/hbtk24o.png" /> ,
|
|
|
|
|
|
| ... | @@ -12,4 +12,29 @@ Picture is borrowed from [there](http://docs.opencv.org/2.4/modules/calib3d/doc/ |
... | @@ -12,4 +12,29 @@ Picture is borrowed from [there](http://docs.opencv.org/2.4/modules/calib3d/doc/ |
|
|
|
|
|
|
|
|
|
|
|
|
### Finding points on laser plane
|
|
### Finding points on laser plane
|
|
|
The equation for pinhole camera is under-determined so we have to find one more condition to estimate the position 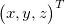 using only projection coordinates 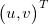. |
|
The equation for pinhole camera is under-determined so we have to find one more condition to estimate the position 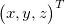 using only projection coordinates 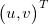. We can use chessboard plane, because OpenCV can find the transformation between those coordinates and camera coordinates. Furthermore, we can say that in chessboard coordinates all points are laying on plane described as z = 0. We are able to transform this plane to camera coordinates like:
|
|
\ No newline at end of file |
|
|
|
|
|
<img src="http://mathurl.com/gw8dwdp.png" /> ,
|
|
|
|
<img src="http://mathurl.com/zwt5qhc.png" />.
|
|
|
|
|
|
|
|
Now we have to obtain normal of this plane and its translation:
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/h23dwzm.png" /> ,
|
|
|
|
<img src="http://mathurl.com/hxa6ykl.png" /> ,
|
|
|
|
<img src="http://mathurl.com/j7y8cdf.png" /> ,
|
|
|
|
|
|
|
|
so the <img src="http://mathurl.com/j865cst.png" />.
|
|
|
|
|
|
|
|
Now we can add this condition to pinhole camera model equation, where [**R**|t] matrix is identity matrix and <img src="http://mathurl.com/j7ltgkr.png" />, we end up with:
|
|
|
|
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/jzqcmgq.png" />
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|