estimate_laser_plane.md

 # Estimation of the Laser Plane position
 ---
-We will use pinhole camera model for finding 3D points in camera coordinates system 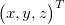![alt text](http://mathurl.com/hj835tq.png) from projection coordinates 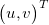![alt text](http://mathurl.com/hw2kh9a.png) described as:
+A pinhole camera model is used for finding 3D points in camera coordinates system 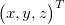![alt text](http://mathurl.com/hj835tq.png) from projection coordinates 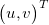![alt text](http://mathurl.com/hw2kh9a.png):
 
 <img src="http://mathurl.com/hbtk24o.png" /> ,
 
-where **K** is the camera matrix from [there](find_camera_mtx), [**R**|t] is transformation matrix and s is a real number parameter.
+where **K** is the camera matrix from [there](find_camera_mtx), [**R**|t] is transformation matrix and s is a scale parameter.
 
 ![pinhole_camera_model](http://gitlab.ciirc.cvut.cz/cmirajak/laser_plane_scanner/uploads/17854790f79da224f708e89ded8d3453/pinhole_camera_model.png)
 
-Picture is borrowed from [there](http://docs.opencv.org/2.4/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html)
+Courtesy [there](http://docs.opencv.org/2.4/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html)
 
 
 ### Inverse transformation of pinhole camera equation
-The equation for pinhole camera is under-determined so we have to add one more condition to estimate the position 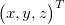![alt text](http://mathurl.com/hj835tq.png) using only projection coordinates 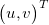![alt text](http://mathurl.com/hw2kh9a.png). OpenCV is able to find the transformation between the chessboard coordinates and the camera coordinates. Hence, we use chessboard plane. Furthermore, we can say that in chessboard coordinates all points are laying on plane described as z = 0. We are able to transform this plane to the camera coordinates like:
+The inverse transformation for picture coordinates to world one is under-determined. One more condition must be added to estimate the position 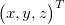![alt text](http://mathurl.com/hj835tq.png) using only projection coordinates 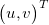![alt text](http://mathurl.com/hw2kh9a.png). OpenCV can find the transformation between the chessboard coordinates and the camera coordinates. Hence, we use chessboard plane. Furthermore, we can say that in chessboard coordinates all points are laying on plane described as z = 0. We can transform this plane to the camera coordinates like:
 
 <img src="http://mathurl.com/gw8dwdp.png" /> ,
 <img src="http://mathurl.com/zwt5qhc.png" />.
@@ -35,19 +35,19 @@ Thereafter, we can make inverse transformation from ![alt text](http://mathurl.c
 
 ### Tracking laser points in image
 
-In first, when we want to track a laser path, we convert an image with the laser path to the gray scale image with custom channel weights. The biggest weight is given to red channel, green one takes one quarter and blue is almost ignored. The following picture is using R:G:B ratio 70:25:5.
+In first, when we want to track a laser path, we convert an image with the laser path to the grayscale image with custom channel weights. The most significant influence is given to red channel, green one takes one quarter, and blue is almost ignored. The following picture is using R:G:B ratio 70:25:5.
 
 ![result_cal_up_gray](http://gitlab.ciirc.cvut.cz/cmirajak/laser_plane_scanner/uploads/6a5bd62aa4bb7f974336439accd5415e/result_cal_up_gray.png)
 
-As you can see on the picture above the laser path has slightly higher intensity then anything around. Therefore, we determine the laser position with pixel precision as the pixel with maximal intensity in some direction (i.e. row/column). 
+As you can see on the picture above the laser path has slightly higher intensity than anything around. Therefore, we determine the laser position with pixel precision as the pixel with maximal intensity in some direction (i.e., row/column). 
 
-To refine it, we know that the laser light should have normal distribution around the maximum. Hence, we choose the specific neighborhood around maximum and calculate logarithm of intensities inside of it. These point are describing some kind of parabola now. Due to that we use LSQ and fit one there. Finally, we call its local maximum as a place with maximal intensity in a specific direction. 
+To refine it, we know that the laser light should have a normal distribution around the maximum. Hence, we choose the specific neighborhood around maximum and calculate the logarithm of intensities inside of it. These points are describing some parabola now. Due to that we use LSQ and fit one there. Finally, we call its local maximum as a place with maximal intensity in a specific direction. 
 
 ### Estimating Laser Plane Position
 
-As you can see on pictures bellow, not all laser points are laying on chessboard so we select the only the one that does and transform them from image points to the camera coordinates.
+As you can see on pictures below, not all laser points are laying on the chessboard, so we select the only the one that does and transforms them from image points to the camera coordinates.
 
-We obtain these points for two different positions of chessboard and get a set of points, which are laying on the laser plane. Thereafter, we fit plane in-between points using singular value decomposition (svd) and receive the laser plane equation as:
+We obtain these points for two different positions of a chessboard and get a set of points, which are laying on the laser plane. After that, we fit plane in-between points using singular value decomposition (svd) and receive the laser plane equation as:
 
 <img src="http://mathurl.com/zw2vhdq.png" />