| ... | ... | @@ -4,7 +4,7 @@ We will use pinhole camera model for finding 3D points in camera coordinate syst |
|
|
|
|
|
|
|
<img src="http://mathurl.com/hbtk24o.png" /> ,
|
|
|
|
|
|
|
|
where **K** is the camera matrix from [there](find_camera_mtx), [**R**|t] is transformation matrix and s is integer number parameter.
|
|
|
|
where **K** is the camera matrix from [there](find_camera_mtx), [**R**|t] is transformation matrix and s is a real number parameter.
|
|
|
|
|
|
|
|

|
|
|
|
|
| ... | ... | @@ -12,12 +12,12 @@ Picture is borrowed from [there](http://docs.opencv.org/2.4/modules/calib3d/doc/ |
|
|
|
|
|
|
|
|
|
|
|
### Inverse transformation of pinhole camera equation
|
|
|
|
The equation for pinhole camera is under-determined so we have to find one more condition to estimate the position 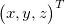 using only projection coordinates 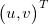. We can use chessboard plane, because OpenCV can find the transformation between those coordinates and camera coordinates. Furthermore, we can say that in chessboard coordinates all points are laying on plane described as z = 0. We are able to transform this plane to camera coordinates like:
|
|
|
|
The equation for pinhole camera is under-determined so we have to add one more condition to estimate the position 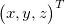 using only projection coordinates 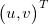. OpenCV is able to find the transformation between the chessboard coordinate and the camera coordinate. Hence, we use chessboard plane. Furthermore, we can say that in chessboard coordinates all points are laying on plane described as z = 0. We are able to transform this plane to the camera coordinate like:
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/gw8dwdp.png" /> ,
|
|
|
|
<img src="http://mathurl.com/zwt5qhc.png" />.
|
|
|
|
|
|
|
|
Now we have to obtain normal of this plane and its translation:
|
|
|
|
Now we have to obtain a normal of plane and its translation:
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/h23dwzm.png" /> ,
|
|
|
|
<img src="http://mathurl.com/hxa6ykl.png" /> ,
|
| ... | ... | @@ -25,7 +25,7 @@ Now we have to obtain normal of this plane and its translation: |
|
|
|
|
|
|
|
so the <img src="http://mathurl.com/j865cst.png" />.
|
|
|
|
|
|
|
|
Now we can add this condition to pinhole camera model equation, where [**R**|t] matrix is identity matrix and <img src="http://mathurl.com/j7ltgkr.png" />, we end up with:
|
|
|
|
Now we can add this condition to the pinhole camera model equation, where [**R**|t] matrix is an identity matrix and <img src="http://mathurl.com/j7ltgkr.png" />, we end up with:
|
|
|
|
|
|
|
|
<img src="http://mathurl.com/jzqcmgq.png" />
|
|
|
|
|
| ... | ... | @@ -33,10 +33,16 @@ Thereafter, we can make inverse transformation from 
|
|
|
|
|
|
|
|
As you can see on the picture above the laser path has slightly higher intensity then anything around. Therefore, we determine the laser position with pixel precision as the pixel with maximal intensity in some direction (i.e. row/column).
|
|
|
|
|
|
|
|
To refine it, we know that the laser light should have normal distribution around the maximum. Hence, we choose the specific neighborhood around maximum and calculate logarithm of intensities inside of it. These point are describing some kind of parabola now. Due to that we use LSQ and fit one there. Finally, we call its local maximum as a place with maximal intensity in specific direction.
|
|
|
|
|
|
|
|

|
|
|
|

|
|
|
|
|