|
|
# Rotation table
|
|
# Rotation table
|
|
|
---
|
|
---
|
|
|
We use rotation table connected to MARS 8 unit for rotating object.
|
|
We use a rotation table connected to the MARS 8 unit for rotating an object.
|
|
|
|
|
|
|
|
## Communication
|
|
## Communication
|
|
|
Communication is done via USB and serial communication module inside the unit (setting and communication commands can be found [there](http://cmp.felk.cvut.cz/~pisa/mars8/mars8_man_cz.pdf)). For easy communication with the unit there is python package called MarsTable, which can perform all necessary operation for you.
|
|
The communication is done via USB and a serial communication module inside the unit (setting and communication commands can be found [there](http://cmp.felk.cvut.cz/~pisa/mars8/mars8_man_cz.pdf)). For easy communication with the unit there is a python package called MarsTable, which can perform all necessary operation for you.
|
|
|
|
|
|
|
|
## Table setting
|
|
## Table setting
|
|
|
Table setting is using a YAML file config as follows:
|
|
The table setting is using an YAML file config as follows:
|
|
|
```yaml
|
|
```
|
|
|
regulator :
|
|
regulator :
|
|
|
P : 200
|
|
P : 200
|
|
|
I : 0
|
|
I : 0
|
| ... | @@ -18,7 +18,7 @@ regulator : |
... | @@ -18,7 +18,7 @@ regulator : |
|
|
---
|
|
---
|
|
|
|
|
|
|
|
## Finding the rotation axis of table
|
|
## Finding the rotation axis of table
|
|
|
The rotation axis can be found when we put the calibration chessboard on table and collect some images with different rotations. Thus, we can find transformations between these boards and camera and determine the rotation axis of table.
|
|
The rotation axis can be found when we put the calibration chessboard on the table and collect some images with different rotations. Thus, we can find transformations between these boards and camera and determine the rotation axis of table.
|
|
|
|
|
|
|
|
We are looking for axis described as direction vector 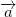 and translation vector 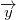.
|
|
We are looking for axis described as direction vector 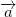 and translation vector 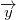.
|
|
|
|
|
|
| ... | @@ -42,4 +42,10 @@ Thus, we end up with: |
... | @@ -42,4 +42,10 @@ Thus, we end up with: |
|
|
|
|
|
|
|
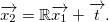
|
|
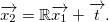
|
|
|
|
|
|
|
|
|
### Direction vector
|
|
|
|
|
|
|
|
Next, we have to find a vector 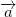. We know that when we move it back to the origin with vector 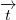. This vector must remind same. So we remain with equation:
|
|
|
|
|
|
|
|
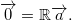
|
|
|
|
|
|
|
|
|
As we can see all eigenvectors of 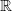 can satisfy this. We calculate them and select the one corresponding to the smallest eigenvalue. |