rotation_table.md

@@ -44,11 +44,11 @@ Thus, we end up with:
 
 ### Direction vector
 
-Next, we have to find a vector 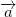![alt text](http://mathurl.com/jm7yc4a.png). We know that when we move it back to the origin with vector 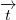![alt text](http://mathurl.com/jntzz6q.png). This vector must remind same. So we remain with equation:
+Next,  we have to find the rotation vector 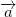![alt text](http://mathurl.com/jm7yc4a.png). We know that, the vector parallel to rotation axis must satisfy: 
 
-![alt text](http://mathurl.com/zjeuyqv.png)
+![alt text](http://mathurl.com/gnw5gey.png).
 
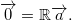
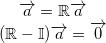-As we can see all eigenvectors of 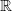![alt text](http://mathurl.com/5unln6.png) can satisfy this. We calculate them and select the one corresponding to the smallest eigenvalue.
+That mean the rotation vector is an eigenvector of the rotation matrix 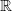![alt text](http://mathurl.com/5unln6.png). Furthermore, the eigenvalues of 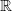![alt text](http://mathurl.com/5unln6.png) are complex conjugate numbers and one number 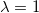![alt text](http://mathurl.com/d33pygb.png). Thus, we use the eigenvector corresponding to 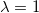![alt text](http://mathurl.com/d33pygb.png) and call it the rotation vector 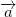![alt text](http://mathurl.com/jm7yc4a.png).
 
 
 ### Translation vector