Skip to content
GitLab

rotation_table · Changes

Page history
cmirajak deleted page: laser_pos_est authored by Cmíral Jakub's avatar Cmíral Jakub
Hide whitespace changes
Inline Side-by-side
rotation_table.md
View page @ f3579816
# Rotation table
---
We use a rotation table connected to the MARS 8 unit for rotating an object.
The rotation table connected to the MARS 8 unit is used. We provided a python package, called `MarsTable`, which controls the MARS unit via USB (Setting and communication commands comes from [refence unit page](http://cmp.felk.cvut.cz/~pisa/mars8/mars8_man_cz.pdf), the documents are available in Czech only).
## Communication
The communication is done via USB and a serial communication module inside the unit (setting and communication commands can be found [there](http://cmp.felk.cvut.cz/~pisa/mars8/mars8_man_cz.pdf)). For easy communication with the unit there is a python package called MarsTable, which can perform all necessary operation for you.
## Table setting
The table setting is using an YAML file config as follows:
#### Table setting
The table setting uses YAML configuration files. The example follows:
```
---
regulator :
A:
P : 200
I : 0
D : 0
......@@ -17,64 +16,59 @@ regulator :
```
---
## Finding the rotation axis of table
The rotation axis can be found when we put the calibration chessboard on the table and collect some images with different rotations. Thus, we can find transformations between these boards and camera and determine the rotation axis of table.
# Rotation axis of the table
The rotation axis of the table is obtained using the calibration pattern. The pattern is placed on the table. The picture of the table with the pattern is taken. The table performs a rotation in the right-handed direction without slipping the pattern. The second image of the table is grabbed.
We are looking for axis described as a direction vector 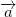![alt text](http://mathurl.com/jm7yc4a.png) and a translation vector 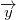![alt text](http://mathurl.com/hrfjerk.png).
[//]: # ( The rotation axis can be found when we put the calibration chessboard on the table and collect some images with different rotations. Thus, we can find transformations between these boards and camera and determine the rotation axis of the table.) We are looking for axis described as a direction vector 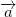![alt text](http://mathurl.com/jm7yc4a.png) and a translation vector 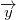![alt text](http://mathurl.com/hrfjerk.png). )
On following image we can see some basic relations between our coordinate systems. All we know are [R|t] transformations between camera coordinates and both board coordinates (green and red).
The basic relations between our coordinate systems are shown in the picture below. Only the transformations transformations [R|t] between camera coordinates and both board coordinates, green and red, are known.
![table_axis](http://gitlab.ciirc.cvut.cz/cmirajak/laser_plane_scanner/uploads/2763c2b2cf5571ddc918ab042ca3aee0/table_axis.png)
### Finding transformation between boards
First, we have to find a transformation between both chessboards as:
First of all, the transformation between both chessboards positions must be found:
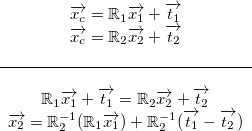![alt text](http://mathurl.com/j4b8k94.png).
As you can see, we will work in the coordinate system of ![alt text](http://mathurl.com/jaeprsg.png).
The coordinate system with the origin ![alt text](http://mathurl.com/jaeprsg.png) is used.
To simplify our equation we will use following identities:
Following identities are used to simplify the equations:
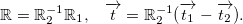
![alt text](http://mathurl.com/jpjc2n7.png)
Thus, we end up with:
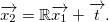
![alt text](http://mathurl.com/jgluop4.png)
### Direction vector
Next, we have to find the rotation vector 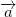![alt text](http://mathurl.com/jm7yc4a.png). We know that, the vector parallel to rotation axis must satisfy:
The direction vectro 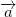![alt text](http://mathurl.com/jm7yc4a.png) is parallel to the rotation plane and do not change its direction after rotation. Thus, it must satisfy following:
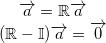![alt text](http://mathurl.com/gnw5gey.png).
That mean the rotation vector is an eigenvector of the rotation matrix 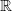![alt text](http://mathurl.com/5unln6.png). Furthermore, the eigenvalues of 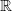![alt text](http://mathurl.com/5unln6.png) are complex conjugate numbers and one number 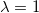![alt text](http://mathurl.com/d33pygb.png). Thus, we use the eigenvector corresponding to 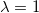![alt text](http://mathurl.com/d33pygb.png) and call it the direction vector 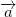![alt text](http://mathurl.com/jm7yc4a.png).
The rotation vector is an eigenvector of the rotation matrix 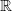![alt text](http://mathurl.com/5unln6.png). Furthermore, the eigenvalues of 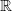![alt text](http://mathurl.com/5unln6.png) are complex conjugate numbers and one real number 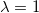![alt text](http://mathurl.com/d33pygb.png). The eigenvector corresponding to 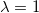![alt text](http://mathurl.com/d33pygb.png) is used and called as the direction vector 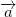![alt text](http://mathurl.com/jm7yc4a.png) (the vector must be normalized).
### Translation vector
As you can see on the picture above when we translate vector 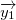![alt text](http://mathurl.com/gwoqjj3.png) by the vector 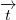![alt text](http://mathurl.com/jntzz6q.png) and rotate it with the rotation matrix 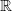![alt text](http://mathurl.com/5unln6.png) we will end-up at same place. To simplify equation we call 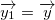![alt text](http://mathurl.com/zeh2wcc.png)
The translate vector 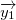![alt text](http://mathurl.com/gwoqjj3.png) is transformed by the vector 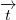![alt text](http://mathurl.com/jntzz6q.png) and rotated it with the rotation matrix 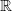![alt text](http://mathurl.com/5unln6.png) it points to the same place as before. The transformation between these two positions is rigid, so it must satisfy following:
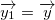
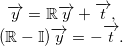
![alt text](http://mathurl.com/zeh2wcc.png)
![alt text](http://mathurl.com/hz8h7pf.png)
However, this equation have multiple solutions in a 3D space. So we must add an other condition to this to clarify the solution. We know that both origins are rotating in a plane with normal vector 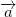![alt text](http://mathurl.com/jm7yc4a.png) from previous. Moreover, the normal vector must be perpendicular with the vector 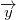![alt text](http://mathurl.com/hrfjerk.png). We can add a following condition:
The equation has multiple solutions in a 3D space, resp. a circle of possible positions of the vector. Another condition must be added to clarify the solution. The direction vector 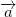![alt text](http://mathurl.com/jm7yc4a.png) must be perpendicular to the translation vector 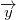![alt text](http://mathurl.com/hrfjerk.png) when the board coordinates are used. The following condition is added:
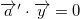
![alt text](http://mathurl.com/hb4t2zq.png)
Now, we are able to write it as a matrix equation:
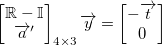
![alt text](http://mathurl.com/jk4j7dp.png)
Previous equation is over-determined so we can't use casual inversion. Therefore, we use pseudo-inversion and receive the wanted solution.
### Translation and direction vector in camera
Previous equation is over-determined and cannot be inverted. The M-P pseudo-inversion is used.
To transform both the direction vector 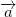![alt text](http://mathurl.com/jm7yc4a.png) and the translation vector 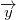![alt text](http://mathurl.com/hrfjerk.png), we use equation:
#### Translation and direction vector in camera
The direction vector 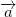![alt text](http://mathurl.com/jm7yc4a.png) and translation vector 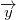![alt text](http://mathurl.com/hrfjerk.png) are in the coordinate system of the pattern. They must be transformed back to the camera system as:
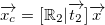![alt text](http://mathurl.com/zpcvd9v.png),
where we replace 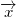![alt text](http://mathurl.com/z29b7za.png) with 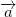![alt text](http://mathurl.com/jm7yc4a.png) or 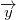![alt text](http://mathurl.com/hrfjerk.png).
## Rotating slice
We use the rotation about arbitrary axis described [here](https://sites.google.com/site/glennmurray/Home/rotation-matrices-and-formulas).
\ No newline at end of file
The rotation about arbitrary axis described [here](https://sites.google.com/site/glennmurray/Home/rotation-matrices-and-formulas) is used.
\ No newline at end of file