| ... | ... | @@ -52,12 +52,11 @@ That mean the rotation vector is an eigenvector of the rotation matrix 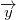 must satisfy that it remain same when transformed. So we get:
|
|
|
|
As you can see on the picture above when we translate vector 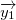 by the vector 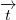 and rotate it with the rotation matrix 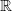 we will end-up at same place. To simplify equation we call 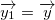
|
|
|
|
|
|
|
|
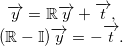
|
|
|
|
|
|
|
|
However, this equation have multiple solution in a 3D space. So we must add an other condition to this to clarify the solution. We know that both origins are rotating in a plane with normal vector 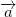 from previous. Moreover, the normal vector must be perpendicular with the vector 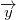. We can add a following condition:
|
|
|
|
However, this equation have multiple solutions in a 3D space. So we must add an other condition to this to clarify the solution. We know that both origins are rotating in a plane with normal vector 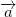 from previous. Moreover, the normal vector must be perpendicular with the vector 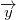. We can add a following condition:
|
|
|
|
|
|
|
|
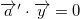
|
|
|
|
|
| ... | ... | |